容许负载
●基本动态额定负载(C)
基本动态额定负载是使一组相同的线性系统在相同的条件下分别行走,其中90%不会因滚动疲劳而产生材料损坏,且以恒定方向行走50×103m时大小一样的负载。
●基本静态额定负载(Co)
基本静态额定负载是指在承受最大应力的接触部分上,滚动体的永久变形量与滚动面的永久变形量之和为滚动体直径的0.0001倍所需的静止负载。
●容许静力矩(M P、M Y、M R)
力矩负载发生作用时所承受的静态力矩负载限值由基本静态额定负载Co与相同的永久变形量决定。
●静态安全系数(fS)
静止时或低速运动时所承受的基本静态额定负载Co根据使用条件,除以表-1所示的静态安全系数fs后使用。
表-1 静态安全系数(fS的下限)
| 使 用 条 件 |
fS的下限 |
| 正常运行条件时 |
1~2 |
| 要求有平滑的移动性能时 |
2~4 |
| 有振动、冲击时 |
3~5 |

fS: 静态安全系数 Co: 基本静态额定负载(N)
MP、MY、MR: 容许静力矩(N・m)
寿命
线性系统在承受负载并进行直线往复运动时,由于重复应力经常作用于滚动体或滚动面上,因此会出现被称为材料疲劳性剥落的鳞状损伤。发生这一最初剥落之前的总行走距离被称作线性系统的寿命。
●额定寿命(L)
额定寿命是指在相同条件下,分别使一群相同的线性系统行走时,其中90%不发生剥落而达到的总行走距离。
额定寿命可根据基本动态额定负载与施加在线性系统上的负载按下列公式求出。

L : 额定寿命(km)
C : 基本动态额定负载(N)
P : 作用负载(N)
●实际使用线性系统时,首先应进行负载计算。要通过计算求出直线往复运动中的负载并不容易,因为运动过程中存在振动或冲击,并且还要充分考虑振动或冲击相对于线性系统的分布状况。另外,使用温度等也会对寿命产生很大影响。将这些条件加在一起,上述计算公式变成下式。

L : 额定寿命(km)
fH : 硬度系数(参见图-1)
C : 基本动态额定负载(N)
fT : 温度系数(参见图-2)
P : 作用负载(N)
fC : 接触系数(参见表-3)
fW : 负载系数(参见表-4)
寿命时间可以通过求出单位时间的行走距离而进行计算。
行程长度和行程次数恒定时,按以下公式求得。

Lh : 寿命时间(hr)
ℓs : 行程长度(m)
L : 额定寿命(km)
n1 : 每分钟往返次数(cpm)
摩擦阻力和必要推力
摩擦阻力(必要推力)可根据负载与系统所固有的密封阻力按下列公式求出。

F : 摩擦阻力(N)
μ : 动摩擦系数
W : 负载
f : 密封阻力(2N~5N)
表-2 动摩擦系数
| 种 类 |
动摩擦系数(μ) |
| 微型直线导轨 |
0.004~0.006 |
| 中载直线导轨 |
0.002~0.003 |
| 线性滑道 |
0.001~0.003 |
| 线性滑台 |
0.001~0.003 |
| 直线轴承 |
0.002~0.003 |
| 线性滚珠衬套 |
0.0006~0.0012 |
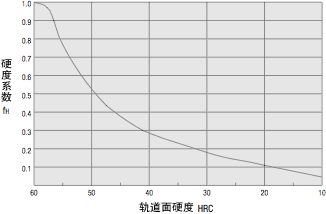
●硬度系数(fH)
使用线性系统时,即使是滚珠接触的轴也必须具有充分的硬度。如果达不到适当的硬度,容许负载将减小,从而缩短使用寿命。
请用硬度系数补正额定寿命。
图-1. 硬度系数
●接触系数(fC)
实际使用线性系统时,通常在1个轴上使用2个以上的线性系统。在这种情况下,施加在各线性系统上的负载因加工精度而异,不会成为均衡负载。其结果,每个线性系统的容许负载会因每个轴上的线性系统数量而异。
请用表-2的接触系数补正额定寿命。
●负载系数(fW)
计算作用于线性系统的负载时,除了物体的重量之外,还必须正确地求出运动速度所产生的惯性力或力矩负载以及它们与时间的变化关系等。但在往复运动中,除了经常重复起动与停止之外,还要考虑到振动、冲击等因素,很难进行正确的计算。
因此,可使用表-3所示的负载系数以简化寿命计算。
